Stefan Fasold's research while affiliated with Vistec Electron Beam GmbH and other places

Metasurfaces are 2D planar lattices of nanoparticles that allow the manipulation of incident light properties. Because of that attribute, metasurfaces are promising candidates to replace bulky optical components. Traditionally, metasurfaces are made from a periodic arrangement of identical unit cells. However, more degrees of freedom are accessible if an increasing number of structured unit cells are combined. The present study explores a type of dielectric metasurface with complex supercells composed of Mie-resonant dielectric nanocylinders and nanoscale rings. We numerically and experimentally demonstrate the signature of an optical response that relies on the structures sustaining staggered optically induced magnetic dipole moments. The optical response is associated with an optical antiferromagnetism. The optical antiferromagnetism exploits the presence of pronounced coupling between dissimilar Mie-resonant dielectric nanoparticles. The coupling is manipulated by engineering the geometry and distance between the nanoparticles, which ultimately enhances their effective magnetic response. Our results suggest possible applications in resonant nanophotonics by broadening the modulation capabilities of metasurfaces.

Conventional optical diffusers, such as thick volume scatterers (Rayleigh scattering) or microstructured surface scatterers (geometric scattering), lack the potential for on-chip integration and are thus incompatible with next-generation photonic devices. Dielectric Huygens' metasurfaces, on the other hand, consist of two-dimensional arrangements of resonant dielectric nanoparticles and therefore constitute a promising material platform for ultra-thin and highly efficient photonic devices. When the nanoparticles are arranged in a random but statistically specific fashion, diffusers with exceptional properties are expected to come within reach. In this contribution, we explore how dielectric Huygens' metasurfaces can be used to implement wavelength-selective diffusers with negligible absorption losses and nearly-Lambertian scattering profiles that are largely independent of the angle and polarization of incident waves. We show that the combination of tailored positional disorder with a carefully-balanced electric and magnetic response of the nanoparticles is an integral requirement for the operation as a diffuser. We experimentally and numerically characterize the directional scattering performance of the proposed metasurfaces and highlight their usability in wavefront-shaping applications. Since our metasurfaces operate on the principles of Mie scattering and are embedded in a glassy environment, they may easily be incorporated in integrated photonic devices, fiber optics, or mechanically robust augmented reality displays. This article is protected by copyright. All rights reserved

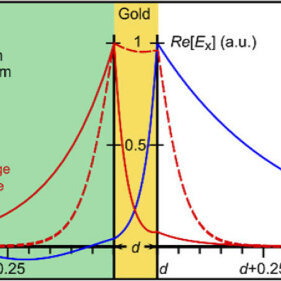
In this study, we explore analytically and experimentally long- and short-range surface plasmon polariton (LR-SPP and SR-SPP, respectively) modes in gold wedges. Especially, we aim to observe the 2-dimensional confinement of the electromagnetic field in gold wedges as it could enhance the light-matter interaction by offering a local density of states which depends on the propagation constant, consequently on the wedge height. The LR-SPP mode can propagate over a long distance, but the real part of the propagation constant remains relatively insensitive to the decreasing wedge height. This mode also experiences cut-off at a wedge height of about 50 nm in our experimental condition. Meanwhile, the SR-SPP mode has a large propagation constant that increases further with decreasing wedge height. As a result, the effective wavelength of the mode shrinks confining the electromagnetic wave longitudinally along the propagation direction in addition to enhancing the transverse confinement of SR-SPP. In the experiment, we use gold wedges with different edge heights to excite each SPP mode individually and image the electromagnetic near field by using a pseudo-heterodyne scattering scanning near-field optical microscope. By imaging the LR-SPP mode field, we demonstrate that the theoretical and measured values of the effective wavelength agree quite well. By using short wedges, we measure the SR-SPP mode field and demonstrate that the effective wavelength decreases to 47% in about half a micrometer of propagation distance. This corresponds to a 3.5 times decrease of the vacuum wavelength or an effective index of 3.5. It is important to note that this value is, by no means, the limit of the electromagnetic field’s longitudinal confinement in a gold wedge. Rather, we were only able to measure the electromagnetic field up to this point due to our measurement limitations. The electromagnetic field will be propagating further, and the longitudinal confinement will increase as well. In conclusion, we measured the SR-SPP in a gold wedge and demonstrate the electromagnetic field confinement in the visible spectrum in gold wedges.

A wide variety of near-field optical phenomena are described by the interaction of dipole radiation with a nanophotonic system. The electromagnetic field due to the dipole excitation is associated with the Green’s function. It is of great interest to investigate the dipole interaction with a photonic system and measure the near-field Green’s function and the quantities it describes, e.g., the local and cross density of optical states. However, measuring the near-field Green’s function requires a point-source excitation and simultaneous near-field detection below the diffraction limit. Conventional single-tip near-field optical microscope (SNOM) provides either a point source excitation or amplitude and phase detection with subwavelength spatial resolution. The automated dual-tip SNOM, composed of two tips, has overcome the experimental challenges for simultaneous near-field excitation and detection. Here, we investigate the dipole emission in the near-field of a dielectric metasurface using the automated dual-tip SNOM. We have analyzed the near-field pattern and directional mode propagation depending on the position of the dipole emission relative to the metasurface. This study is one further step toward measuring the dyadic Green’s function and related quantities such as cross density of optical states in complex nanophotonic systems for both visible and near-infrared spectra.

We experimentally realize a series of incommensurable metasurface stacks that transition from near-field coupling to a far-field regime. Based on a comparison between a semi-analytic model and measurements, we, furthermore, present an experimental study on the validity of the fundamental mode approximation (FMA). As the FMA is a condition for the homogeneity of a metasurface, its validity allows for strong simplification in the design of stacked metasurfaces. Based on this, we demonstrate a method for the semi-analytic design of stacked periodic metasurfaces with arbitrary period ratios. In particular, incommensurable ratios require computational domains of impractically large sizes and are usually very challenging to fabricate. This results in a noticeable gap in parameter space when optimizing metasurface stacks for specific optical features. Here, we aim to close that gap by utilizing the principles of the FMA, allowing for additional parameter combinations in metasurface design.